近日，中国工业与应用数学学会第22届年会（CSIAM 2024）在南京召开，南方科技大学理学院数学系2024级博士生彭漫婷的研究论文“OEDG: Oscillation-eliminating discontinuous Galerkin method for hyperbolic conservation laws”入选第八届CSIAM学生论坛口头报告，并被评为“优秀报告”。

        抑制伪振荡是设计双曲守恒律可靠高精度数值格式中的关键科学问题，过去数十年里吸引了大量数学家和计算流体力学家的关注，其中包括至少8位国际数学家大会(ICM)报告人。彭漫婷的论文提出了一种新颖、稳健且高效的消除振荡的间断 Galerkin（OEDG）方法，通过设计创新性的交替演化机制，结合传统的半离散DG方法和一个阻尼方程，在每个 Runge-Kutta 演化阶段后嵌入一个抑制数值振荡的  OE（Oscillation-Eliminating）过程。基于理论分析，该论文设计了具备重要尺度不变性和演化不变性的阻尼算子。对于线性标量守恒律，该论文严格证明了全离散 OEDG 方法的最优误差估计，这是首次对具有自动振荡控制机制的非线性DG方法进行全离散误差估计。

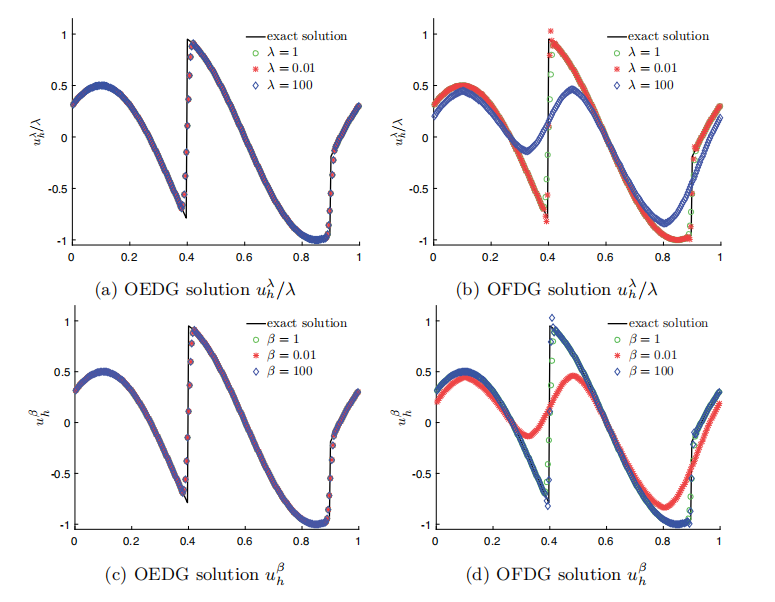
        OEDG方法具有许多显著优点：对于不同尺度和波速的复杂问题，OEDG方法在消除伪振荡方面表现卓越，且不依赖问题的人工参数；对于双曲方程组，无需复杂的特征分解；OEDG方法继承了传统DG方法的关键特性，如局部守恒、最优收敛率和超收敛。由于所提出的阻尼方程可精确求解，OEDG方法在正常的CFL条件下保持稳定性（即使面对强激波引起的高度刚性阻尼项）。尤其突出的是，OE过程是非侵入式的，可作为独立模块简单高效地集成到现有的DG程序中；其实现非常简便，仅需在模态系数上乘以一个阻尼因子。OEDG方法为振荡控制的阻尼机制提供了新的见解，揭示了阻尼技术本质上是一种模态滤波器，并首次建立了阻尼技术与谱粘性技术之间的紧密联系。大量的数值结果验证了OEDG方法的有效性。

        该论文由彭漫婷和导师数学系副教授吴开亮以及阿拉巴马大学助理教授孙铮合作完成，于2024年发表在计算数学学术期刊Mathematics of Computation上。彭漫婷为论文第一作者，吴开亮为通讯作者，南方科技大学数学系为第一署名单位，南方科技大学数学系和深圳国际数学中心为通讯单位。

        中国工业与应用数学学会年会是国内应用数学领域层次高、规模大、影响广的学术盛会之一。本次年会全国仅6人获此荣誉，彭漫婷的获奖展现了南科学子勇于探索、追求卓越的学术风貌。